Imagine you have a set of points on a grid. Then a "transformation" maps (or moves) those points onto a new grid. Each point will transform to a new point. A Linear Transformation is a type of transformation that has certain properties, that will allow us to represent it with a matrix.
Prerequisites
It's essential to already know about:
Introductory Example
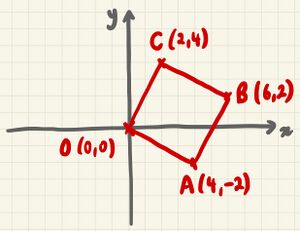
We will transform the square in Figure 1 with the matrix [1].
In this topic, a linear transformation and a matrix are the same thing. The matrix T is the linear transformation T and the linear transformation T is the matrix T.[2]
Transforming one Point
In order to transform point A:
- we'll first write point A as a position vector:
- we pre-multiply by the transformation matrix T:
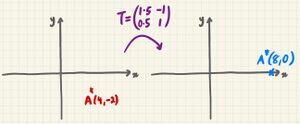
That's it! is the "transformed" . The point (4,-2) has been transformed to (8,0).
Object and Image
In order to avoid confusion, it's common to name the start point "the object A" and name the end point "the image of A". If we start with the object , we may use to represent its image.
Transforming the Origin
One of the rules of Linear Transformations is that the origin won't move.
Notice:
The image of the origin is still the origin. In other words, in a linear transformation, the origin is always an invariant point.
Transforming Multiple Points at once
We could transform points A(4,-2), B(6,2) and C(2,4) one-by-one, by writing them each as position vectors
Or, we could merge them into a single matrix:
Then, pre-multiplying by the matrix T:
Working column-by-column, we see that:
- has transformed to , which we already found earlier,
- has transformed to ,
- has transformed to .
Outcome
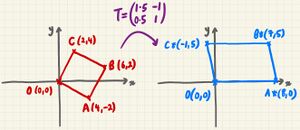
By drawing the new points, we see that the square OABC has been transformed onto the parallelogram OA*B*C*. It's sort of been both stretched and rotated.
"Linear" transformations generally transform straight lines onto new straight lines[3], so it's safe to join the new points with straight lines - in fact, the midpoint of AB will be transformed to the midpoint of A*B*.
Technical Detail
Technically, a linear transformation goes from a vector space[4] to another vector space. At A-Level, the only vector spaces we know are coordinate grids, so we're considering only 2D and 3D coordinate grids.
Linear transformation have the properties that they preserve addition of vectors and preserve scalar multiplication. In other words:
- If , then
This should match our understanding of the algebra of matrices and vectors, making matrices perfect for representing linear transformations.
Next Steps
- Lines of Invariant Points, Invariant Lines
- Types of Linear Transformation
- Combinations of Linear Transformations
- Area and Volume in Linear Transformations
Footnotes
- ↑ It's common to use T or M for a transformation matrix - any capital letter to represent a matrix is possible.
- ↑ If we strongly need to distinguish, we might say that M is the matrix representing linear transformation T.
- ↑ unless the whole line is squashed onto the origin.
- ↑ Literally: any space where vectors exist.