Lines of Invariant Points, Invariant Lines

Invariant means something that doesn't change. A Linear Transformation will transform all the points on a grid, but invariant points will remain in their original position. We will look at invariant points, lines of invariant points, and invariant lines under linear transformations.

Prerequisites

You'll need to have an understanding of Linear Transformations.

Alternative Methods

Eigenvalues and eigenvectors may act as a more practical alternative method here, that will also work well in higher dimensions.

Invariant Points

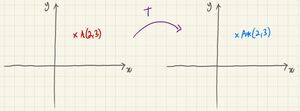
Say we have a linear transformation represented by matrix $M$ . Then, an invariant point is any point which stays the same under the transformation.

In other words, the point A with position vector $\underline{x}$ is invariant if $M \underline{x} = \underline{x} (*)$ .

Since position vector $\underline{x}$ is really shorthand (in 2-dimensions) for $(\begin{matrix} x \\ y \end{matrix})$ , it can be clearer to write this as $M (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} x \\ y \end{matrix})$ .

In 3-dimensions, no problem: we could say $M (\begin{matrix} x \\ y \\ z \end{matrix}) = (\begin{matrix} x \\ y \\ z \end{matrix})$ .

For example, let's consider the matrix $M = (\begin{matrix} 2 & 4 \\ 1 & 5 \end{matrix})$ and the point $B (4, - 1)$ .

We observe that $(\begin{matrix} 2 & 4 \\ 1 & 5 \end{matrix}) (\begin{matrix} 4 \\ - 1 \end{matrix}) = (\begin{matrix} 4 \\ - 1 \end{matrix})$ .

Therefore, B(4,-1) is an invariant point (under the linear transformation M). The image of point B is B itself.

Note that the origin (0,0) is always an invariant point - this is a property of linear transformations.

Lines of invariant points

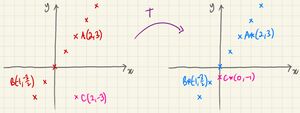
A line of invariant points is a straight line where all the points are invariant.

The word 'invariant' applies to the individual points here - which happen to form a line.

With a few exceptions^[1], a line of invariant points must normally pass through the origin, so we can give it the (2 dimensional) equation $y = m x$ .

By taking the equation $(*)$ above, and substituting $y = m x$ , we can say: $M (\begin{matrix} x \\ m x \end{matrix}) = (\begin{matrix} x \\ m x \end{matrix})$

Invariant Lines

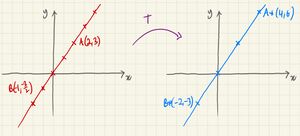
When we say invariant line, we mean that the line stays the same. But, the points on the line could move along the line. The individual points can change - there don't have to be invariant points.

In an invariant line through the origin, it will look like we are stretching out the points along the line, away from (or towards) the origin.

The point $(x_{0}, y_{0})$ , on the line, will move to $(x_{1}, y_{1})$ , also on the line.

If we are talking about the line through the origin, $y = m x$ , we can say $(x_{0}, m x_{0})$ will transform to $(x_{1}, m x_{1})$ .

This gives us a method for finding invariant lines. Solve $M (\begin{matrix} x_{0} \\ m x_{0} \end{matrix}) = (\begin{matrix} x_{1} \\ m x_{1} \end{matrix})$ .

Special Case: Invariant Lines (not necessarily through the origin)

The invariant lines which do not go through the origin are less relevant to higher-level Linear Algebra problems, not counting towards subspaces or eigenvectors, and as such are often ignored. However, these have been used as a source for recent exam questions in A-Level Further Maths (UK), unfortunately.

Sometimes you can quickly identify other invariant lines by thinking about the type of transformation. For example, in a reflection, then all lines perpendicular to the 'mirror' line of symmetry will be invariant.

If you need a proof to find "all invariant lines" for A-Level Further Maths (UK), you may want to start instead with $y = m x + c$ , as follows:
Solve $M (\begin{matrix} x_{0} \\ m x_{0} + c \end{matrix}) = (\begin{matrix} x_{1} \\ m x_{1} + c \end{matrix})$ .

Special Case: Invariant Lines (Vertical)

Note that this method for finding invariant lines won't be capable of finding vertical invariant lines, since vertical lines are of the form $x = k$ , and form an exception to the general form of the equation of a line, $y = m x + c$ .

An eigenvectors method will have no problem finding vertical eigenvectors, since vertical vectors are not exceptions to the general form of vectors. And, finding an eigenvector will imply there is an invariant line, through the origin, in the same direction.

Matrices of the form $M = (\begin{matrix} P & 0 \\ R & S \end{matrix})$ will have at least one vertical invariant line.

A technical proof here could use $T (\begin{matrix} x_{0} \\ y_{0} \end{matrix}) = (\begin{matrix} x_{1} \\ y_{1} \end{matrix})$ could set $x_{0} = x_{1} = k$ , hoping to find values of $k$ independent of $y_{0}$ .

Examples

Example: Finding two invariant lines

Example: Find the two invariant lines in the linear transformation represented by T = $(\begin{matrix} 3 & 2 \\ 2 & 3 \end{matrix})$ .

Since this is a linear transformation with a finite number of invariant lines, let's go ahead and assume that relevant lines include the origin. So, any such lines will be of the form $y = m x$ , which means we can avoid working with $+ c$ as an unknown. There are exceptions to this, but it makes sense to first identify lines which pass through the origin.

Now, for any point, $T (\begin{matrix} x_{0} \\ y_{0} \end{matrix}) = (\begin{matrix} x_{1} \\ y_{1} \end{matrix})$ .

Therefore, for a point on an invariant line, $(\begin{matrix} 3 & 2 \\ 2 & 3 \end{matrix}) (\begin{matrix} x_{0} \\ m x_{0} \end{matrix}) = (\begin{matrix} x_{1} \\ m x_{1} \end{matrix})$

Multiplying out the matrices, we get two equations:

$\begin{aligned} 3 x_{0} + 2 m x_{0} & = & x_{1} & (1) \\ 2 x_{0} + 3 m x_{0} & = & m x_{1} & (2) \end{aligned}$

And substituting $x_{1}$ from $(1)$ into $(2)$ :

$\begin{aligned} 2 x_{0} + 3 m x_{0} & = & m (3 x_{0} + 2 m x_{0}) \\ ⟹ & 2 x_{0} + 3 m x_{0} & = & 3 m x_{0} + 2 m^{2} x_{0} \end{aligned}$

Notice that all the terms now contain $x_{0}$ . Since the case when $x_{0} = 0$ will represent the origin, which we are not looking for here, we can divide both sides by $x_{0}$ (alternatively: compare coefficients of $x_{0}$ ):

$\begin{aligned} ⟹ & 2 + 3 m & = & 3 m + 2 m^{2} \\ ⟹ & 2 m^{2} & = & 2 \\ ⟹ & m^{2} & = & 1 \end{aligned}$

$⟹ m = 1 or m = - 1$

Therefore, our invariant lines are $y = x$ and $y = - x$ .

Example: Proving you have found all invariant lines

Example: Determine the equations of all invariant lines of the transformation represented by M = $(\begin{matrix} 17 & 2 \\ 32 & 5 \end{matrix})$ .

For a proof, we will adapt the above method, assuming that an initial point $(x_{0}, y_{0})$ on the line $y = m x + c$ will move to a new point $(x_{1}, y_{1})$ on the same line.

$\begin{aligned} M (\begin{matrix} x_{0} \\ y_{0} \end{matrix}) & = & (\begin{matrix} x_{1} \\ y_{1} \end{matrix}) \\ ⟹ & M (\begin{matrix} x_{0} \\ m x_{0} + c \end{matrix}) & = & (\begin{matrix} x_{1} \\ m x_{1} + c \end{matrix}) \\ ⟹ & (\begin{matrix} 17 & 2 \\ 32 & 5 \end{matrix}) (\begin{matrix} x_{0} \\ m x_{0} + c \end{matrix}) & = & (\begin{matrix} x_{1} \\ m x_{1} + c \end{matrix}) \\ ⟹ & 17 x_{0} + 2 m x_{0} + 2 c & = & x_{1} & (1) \\ and & 32 x_{0} + 5 m x_{0} + 5 c & = & m x_{1} + c & (2) \\ ⟹ & 32 x_{0} + 5 m x_{0} + 5 c & = & m (17 x_{0} + 2 m x_{0} + 2 c) + c \\ ⟹ & 0 & = & x_{0} (2 m^{2} + 12 m - 32) + c (2 m - 4) \end{aligned}$

Since we can gather that this is true for all $x_{0}$ (in order to form a line), we can compare coefficients of $x_{0}$ :

$\begin{aligned} ⟹ & 2 m^{2} - 12 m - 32 & = & 0 \\ ⟹ & m^{2} - 6 m - 16 & = & 0 \\ ⟹ & m = - 8 or m = 2 \end{aligned}$

And, comparing the constant terms:

$\begin{aligned} c (2 m - 4) = 0 \\ ⟹ & c = 0 or m = 2 \end{aligned}$

Combining both of these leads to the conclusion that,

$\begin{aligned} m & = & - 8 & and & c = 0 & , or \\ m & = & 2 & and & c \in ℝ \end{aligned}$

$\begin{aligned} ⟹ & y & = & - 8 x & or \\ y & = & 2 x + c, c \in ℝ \end{aligned}$

Footnotes

↑ Exceptions include the identity transformation - which is invariant everywhere, and shears, which are invariant for sets of parallel lines. In both cases, you can find a line of invariant points passing through the origin.

[1] Exceptions include the identity transformation - which is invariant everywhere, and shears, which are invariant for sets of parallel lines. In both cases, you can find a line of invariant points passing through the origin.

[1]