Content:Combinations of Linear Transformations

A linear transformation moves points from an xy-grid onto new locations on the xy-grid, according to a transformation matrix M.

We know certain basic types of transformation that are relatively easy to understand and work with. For example: enlargement, reflection, rotation, shear.
We can combine these to build a composite transformation by applying a sequence of these basic transformations.

Prerequisites

We'll assume you already know about:

• Matrix Multiplication
• Linear Transformations

Order Matters!

Transformation T is a shear, and transformation U is a reflection. Applying transformation UT, the shear followed by reflection, gives a different result than applying transformation TU, the reflection followed by the shear.

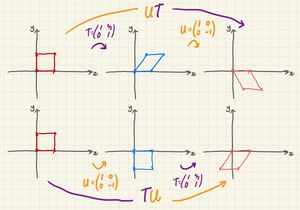
First of all, it's important to note that the order of a sequence of transformations matters - like matrix multiplication, it is NOT commutative. If you change the order of transformations, you will typically get different results.

If we do a shear followed by a reflection, that will give different results than a reflection followed by a shear.

Sequence of two transformations

Suppose we have two transformation matrices $A$ and $B$, and a point with coordinates $(x,y)$, which we'll represent in position vector form: ${\begin{pmatrix}x\\y\end{pmatrix}}$.

We want to apply the two transformation matrices one-by-one: first A, then B.

To apply transformation A, we need to pre-multiply by the matrix A, so $A{\begin{pmatrix}x\\y\end{pmatrix}}$.

To then apply a second transformation matrix $B$, this also has to be pre-multiplied. $B$ will go in first place: $BA{\begin{pmatrix}x\\y\end{pmatrix}}$.

Note that matrix multiplication is not commutative - so we cannot swap the order of $B$ and $A$. $B$ must come before $A$.

However, matrix multiplication is associative - we can process the multiplications in two different orders:

• first calculate $A{\begin{pmatrix}x\\y\end{pmatrix}}$ and then pre-multiply by B, giving $BA{\begin{pmatrix}x\\y\end{pmatrix}}$, or,
• first calculate $BA$ and then pre-multiply $BA$ by ${\begin{pmatrix}x\\y\end{pmatrix}}$, also giving $BA{\begin{pmatrix}x\\y\end{pmatrix}}$.

Two Transformations in One

The transformation $A$ followed by the transformation $B$ can be represented by the transformation $BA$ (note the order!).

We could now think about this as the single composite transformation $BA$.

Interpreting Composite Transformations: Order Matters

When we have a composite transformation, such as $BA$, we may want to think about it also as a sequence. The transformation closest to the position vector ${\begin{pmatrix}x\\y\end{pmatrix}}$ always happens first in the sequence.

When we apply the composite transformation, we have to pre-multiply by $BA$, giving: $BA{\begin{pmatrix}x\\y\end{pmatrix}}$.

Thinking about the decomposed transformations $A$ and $B$ , we see $A$ is closest to the position vector, so we know transformation $A$ happens first. Then, transformation $B$ happens second.

Next Steps

• Lines of Invariant Points, Invariant Lines
• Types of Linear Transformation
• Combinations of Linear Transformations
• Area and Volume in Linear Transformations