Entrance Exams: MAT, TMUA, STEP – Last Minute Topic Tips!
| More Posts by Ronald | |
|---|---|
This is copied from my old blog (2023), for students applying to universities.
It's University Entrance exam season!
This week, a few thousand students are sitting the 2023 edition of the "Mathematical Admissions Test" (MAT), for admission to Mathematics-based undergraduate courses at Oxford, Imperial and Warwick.
Also this week, the last ever "Test of Mathematics for University Admissions" (TMUA) is taking place, for maths-y courses around UK universities, including Computer Science at Cambridge.
These types of tests often make a similar claim - you won't need any more maths than the first year of an A-Level course, or even just GCSE Maths! Do you think it will be that easy to pass? (It is not that easy.) Read on, for 5 syllabus tips that will immediately improve your score...
The MAT, TMUA and STEP exams each have their own slightly-different style. Each test will need its own specific preparation. I strongly recommend trying every past paper you can find, in exam conditions, and then reviewing your answers. Spend time figuring out what they are looking for and how you can boost your scores. At first, a 2.5 hour paper might need 5 hours of intensive study, or longer. With plenty of past papers available online, this is going to need a big commitment of time.
The common theme is that these papers test the depth of your mathematical understanding. Have you understood perfectly, or do you hold any misconceptions? You can expect to be tricked. You will need to anticipate every trick, to face down every exception and every counter-intuitive question. You will need a whole bunch of time-saving methods up your sleeves. Your goal is to feel the satisfaction of seeing through the examiner's tricks, giving fantastic answers to impossible questions.
A problem, then, is that most school courses are not focused on mathemagical trickery. Not at all. The important thing, for school, is to get everyone else through the regular A-Level exam. If you depend on a couple of school-teachers or a single textbook, you might not ever see the types of tricky edge cases or awkward questions that the MAT throws at you. So, you will need to study more widely than just relying on your classroom work.
Since it's close to exam day, while I'm writing this, I'm gonna hope and assume that you have already done some of that work. And, I'll offer you my last-minute tips on 5 topics:
Factor Theorem and the Rational Root Theorem
As soon as you see a polynomial, you can start to think about the Factor Theorem. Lots of students immediately forget that it exists. This leads to either bombing out of a question that needs it, or facing a long and annoying process to get around it. Please, remember the Factor Theorem.
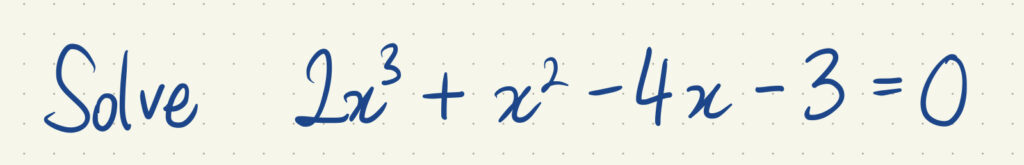
If there's a cubic (or larger) polynomial to solve, we probably should try to factorise it. So, the Factor Theorem helps. Plug in a bunch of numbers k and, if you get 0, then you know (x-k) is your first factor. As long as you know any way to divide polynomials, you are already down to a quadratic. Let's go!
Never have any luck picking a k that works? There's a little off-syllabus helper that you can use, the Rational Root Theorem. As long as all the coefficients are integers, we only need to look at the last coefficient (-3) and the first coefficient (2), and the factors of those (including 1). The only ks that can work must look like "±factor of last coefficient/factor of first coefficient".
This gives us eight sensible options for k: 1, -1, 3, -3, 1/2, -1/2, 3/2, -3/2.
As soon as you find one that works, you can get started with your factorisation.
If none of these work? The Rational Root Theorem tells us that nothing will work: there are no linear factors. Probably, something else is going on.
Multiplying out three brackets
To multiply two brackets, every term in the first brackets gets multiplied by every term in the second brackets. Every combination of terms gets multiplied. Any other shortcut, like "FOIL", will stop working as soon as the brackets get a tiny bit more complicated.
If we have three brackets, what then? I've got two ways, and you might need both:
Method one. Multiply out two brackets, and then multiply the third bracket.
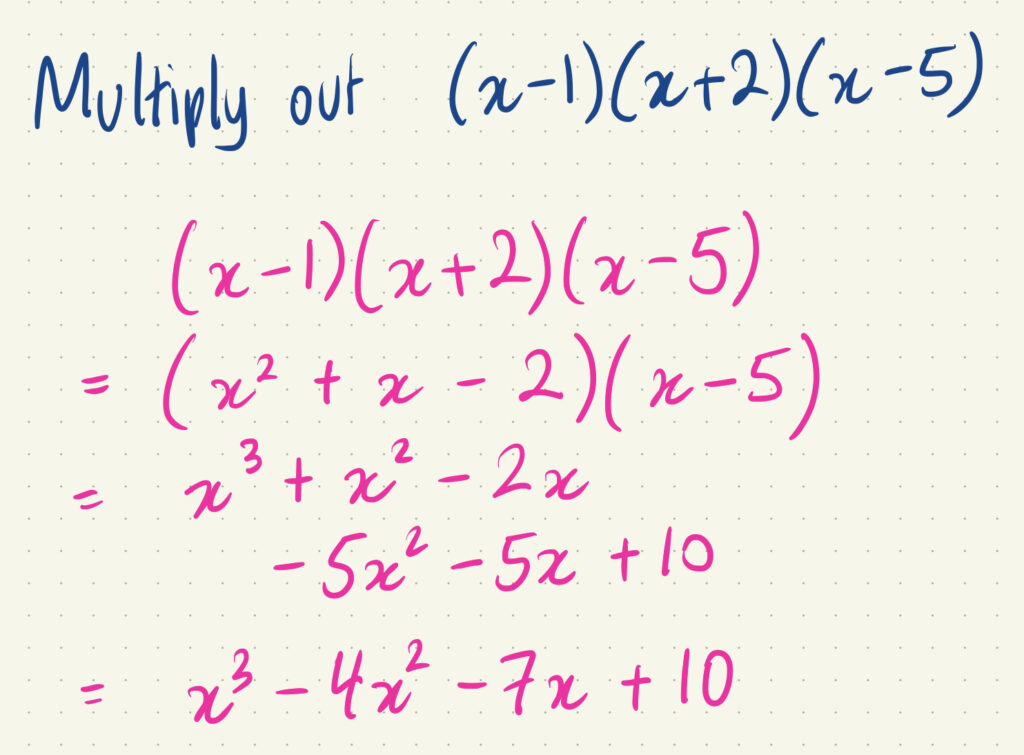
I think it's obvious what to do here. Since there's a bit of administrative work with some risks, you should immediately check your answer: by using the Factor Theorem!
Method two. Take one term from each bracket.
If you've ever seen a Disney Sing-Along film, you know the score here.
Like Mickey Mouse's head keeping track of the lyrics, we're gonna bounce from one bracket to the next, taking one term from each bracket.
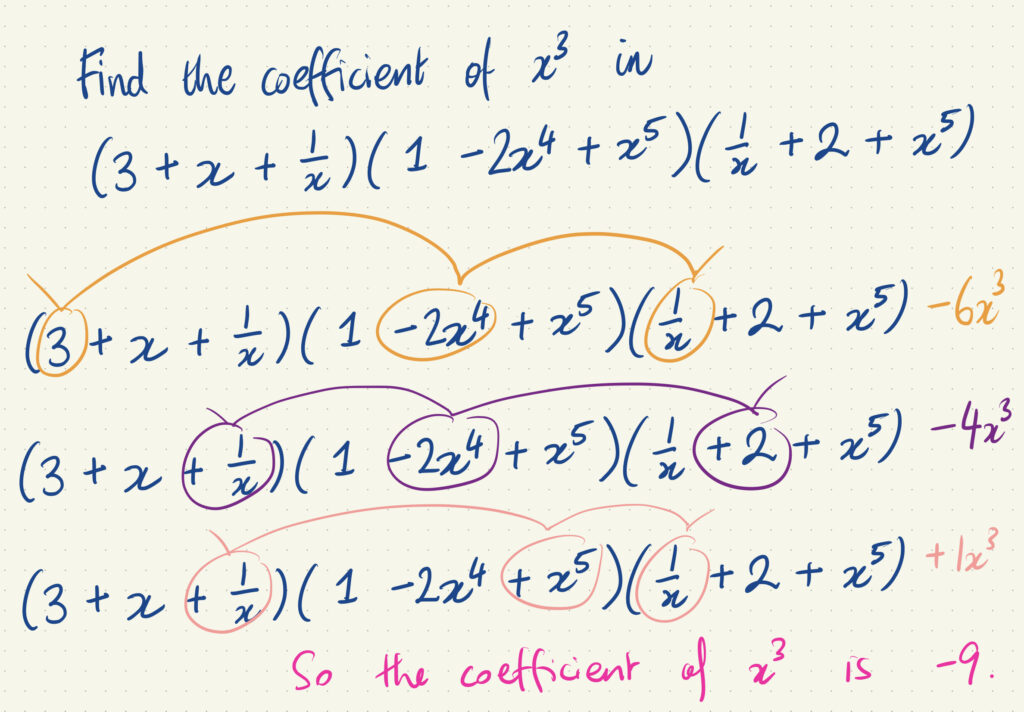
If we multiplied out these three brackets fully, we'd have to bounce across every combination, ending up with 27 terms to collect together. But, maybe, we can target just the few terms that we need - saving a lot of time and administrative work.
How many arrangements?
How many arrangements is a fundamental question of combinatorics. How many arrangements of AABB are there? AABB, ABAB, ABBA, BAAB, BABA, BBAA, so 6 ways. Six is fine, but this number can get huge! So, we need a short-cut.
I'm gonna let you figure out the rule, with only five examples:
- How many arrangements are there of ABCD? 4 factorial = .
- How many arrangements are there of ABCC? .
- How many arrangements are there of AABB? . (This is also or ).
- How many arrangements are there of AABBBC? .
- How many arrangements are there of ABCDBCDCDD? = we don't have a calculator so probably we aren't gonna need to evaluate this.
Got it? Here's a challenging question, to make sure:
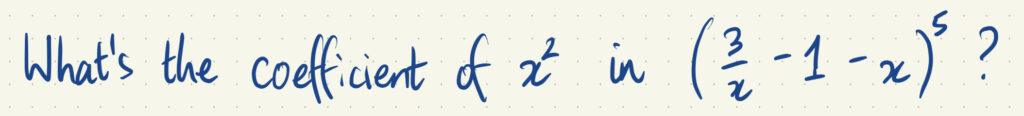
"Show that" with inequalities
Probably, you know a good method to "show that" for equations and identities, e.g.
I would start with one side, usually the left-hand-side. I work my way down the page, with equals signs joining each line. Finally, I reach the right-hand-side, which only appears in the last line of my working. QED.
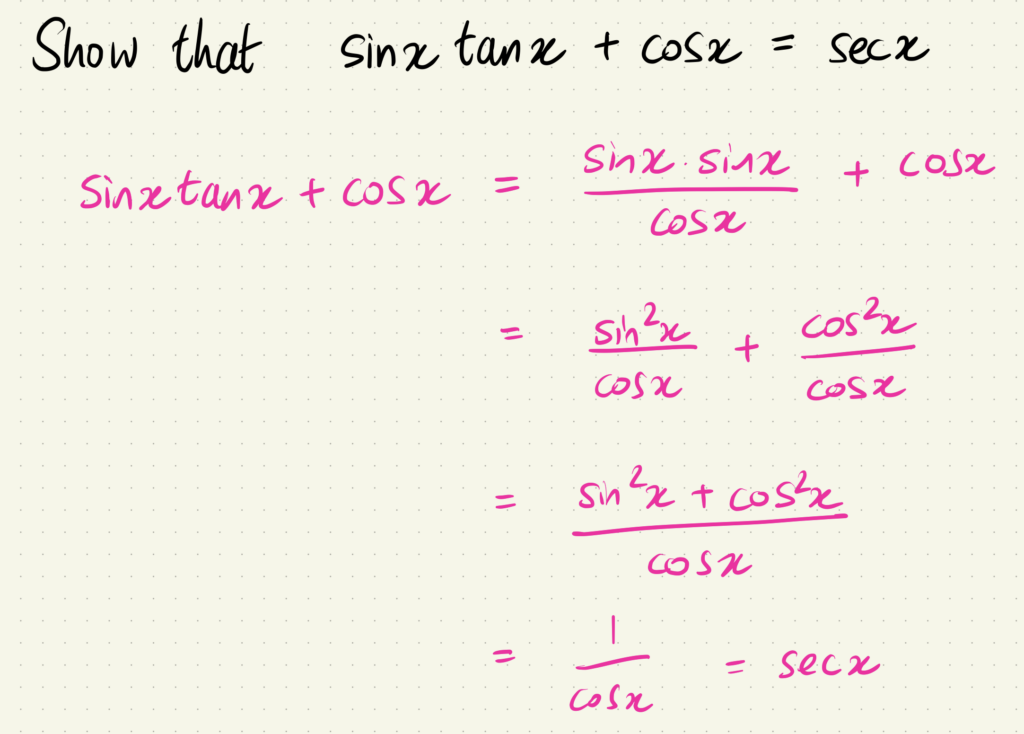
Now, can you "show that" ?
The method is the same, starting with one side, working your way forwards down the page, and finally reaching the other side. But now, to connect your lines of working down the page, you're allowed to use equals signs OR inequality signs (pointing in the right direction).

Phantom solutions
To solve an equation, you can always "do the same thing to both sides". You can do that, as long as you don't divide by anything that could be zero. And, as long as you stick in a sign when you square root both sides. And, as long as you consider multiple solutions for . And,... you might start to think that our high school method of solving equations is a bit broken.
Don't worry too much: there is logic here, somewhere.
But, even if you understand the logic perfectly, it's best to be cautious about 'phantom' solutions, aka 'extraneous' solutions, aka 'spurious' solutions. These extra solutions will randomly arrive as a result of your (correct) algebraic manipulation, but they just don't belong. You gotta check each of your solutions back against the question, and cross out the ones that don't work.

There are certain types of equations that you should be especially cautious about. For example:
- equations with square roots (or even-power roots)
- equations with logarithms
- equations with modulus signs
- equations with algebraic fractions!
- and possibly others 😅
Here are two questions which might look the same, but do not give the same solutions:
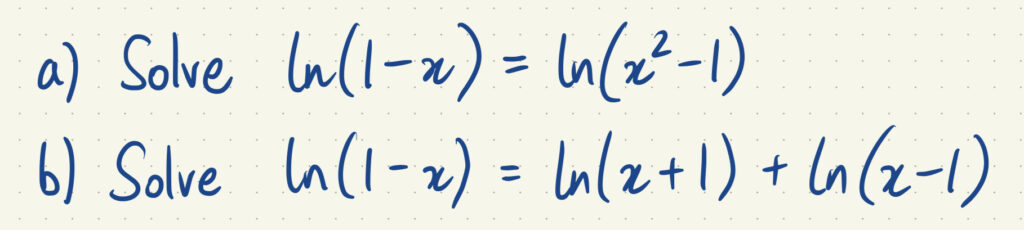
My advice is simple: no matter what equation, plug all your solutions into the original equation to see if they will still work. Always check your work!
Good luck, if you're taking the MAT and TMUA this week.
Do you want some personal help with the MAT, TMUA or STEP math admissions tests? I can help guide you through the process. My tutoring work is personally tailored to fit what you need.
Let me know at ronald@mathswithronald.com and we can arrange a pack of sessions.